旅人算の解き方、受験でよくでる算数・数学の問題

2022年7月27日2023年9月27日

旅人算は速さに関する問題。受験、入試問題で出題されるので小学生・中学生は理解して解けるようにならなければなりません。しかしコツがわかれば楽に解くことができます。

旅人算

本ページはプロモーションが含まれています

追いつき追い越す

これから２つの文章問題を解いていきます。１つ目の文章問題は基本問題、２つ目の文章問題はやや難しい問題です。解説を見ながら旅人算を解くコツを身につけて下さい。

動画による詳しい解説は こちら（クリック）↓

【問題】分速６０mの速さで歩く由美さんが出発してから３０分後に直哉君が分速１５０mの速さで追いかけます。直哉君が由美さんに追いつくのは、直哉君が出発してから何分後でしょう。

次の２つの考え方があります。

（１）差に着目する

直哉君が出発する時、由美さんは既に３０分歩いているので、６０×３０＝１８００（m）先にいます。つまり差は１８００mです。直哉君が由美さんに追いつくのは差が０mになる時です。

２人の速さの差は、１５０－６０＝９０（m/分）

つまり１分間に直哉君の方が９０m長く進みます。

ということは、２人の差は１分間に９０m縮まります。

１８００mの差が１分間に９０m縮まるので、
差が０になる、すなわち直哉君が由美さんに追いつくのは

１８００÷９０＝２０　　答え．２０分後

（２）進んだ距離に着目する

直哉君が由美さんに追いつく時は、２人の進んだ距離が等しい状態です。

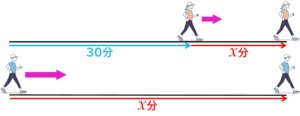
直哉君が由美さんに x分後追いついた時、　　　　　　　　　

直哉君が進んだ距離は　１５０×x （m）

由美さんは直哉君より３０分多く歩いているので

由美さんが進んだ距離は　６０×(３０＋x)（m）

２人が進んだ距離は等しいので

１５０×x ＝ ６０×(３０＋x)

１５０x ＝ １８００＋６０x

９０x ＝ １８００

x ＝ ２０　　答え．２０分後

（クリック）↓↓

【問題】由美さんは午前１０時に、分速６０ｍで家から駅へ向かいました。
その後、兄の直哉君は午前１０時１５分に、分速１５０ｍで家から駅へ向かいました。
直哉君は由美さんを途中で追い越し、由美さんよりも９分早く駅へ着きました。

（１）直哉君が由美さんに追いついたのは何時何分ですか。

（２）家から駅までの距離は何ｍですか。

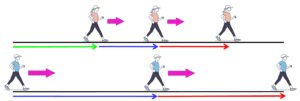
上図の
◆緑の線は直哉君が家を出るまでに由美さんが進んだ距離
◆青の線は直哉君が家を出て由美さんに追いつくまでに進んだ距離
◆赤の線は直哉君が由美さんを追い越してから駅に着くまでに進んだ距離
を表しています。

【解答】

（１）直哉君が由美さんに追いついたのは何時何分ですか。

由美さんは１０時、直哉君は１０時１５分に家を出ましたので、直哉君が出る時由美さんは既に１５分進んでいます。

６０×１５＝９００（ｍ）

直哉君が家を出る時由美さんとの距離は９００ｍです。

２人の速さの差は

１５０－６０＝９０

よって１分で９０ｍ差が縮まります。

９００÷９０＝１０

直哉君は１０分後に追いつきますので

１０時１５分＋１０分＝１０時２５分

答え．午前１０時２５分

（２）家から駅までの距離は何ｍですか。

直哉君は由美さんより９分早く駅へ着いたということは、直哉君が駅へ着いてから由美さんは９分進んで駅へ着いたということです。

由美さんが９分間に進む距離は５４０ｍです。

６０×９＝５４０

ですから直哉君が駅へ着いた時由美さんとの距離の差が５４０mだったのです。

直哉君が由美さんに追いついたとき２人は同じ場所にいたので、それから５４０ｍ差がつくには何分かかるかを計算すれば、直哉君が由美さんを追い越してから何分後に駅へ着いたのかがわかります。

１５０－６０＝９０

直哉君（１５０ｍ/分）と由美さん（６０ｍ/分）は１分間に９０mの差がつきます。

５４０÷９０＝６

５４０ｍの差がつくのは６分後です。

直哉君は由美さんに追いつくまで１０分、追い越してから駅まで６分、合計１６分進みました。

１５０×１６＝２４００

直哉君は２４００m進んで駅へ着きました。

答え．２４００ｍ

以上のように旅人算を解く時は２人の位置関係を簡単な図に表すと、解きやすくなります。

基本から着実に理解して
格段に成績を伸ばす「すらら」↓

あわせて読みたい

速さに関する文章問題を解くコツ も読んでみて下さい。

あわせて読みたい

通過算、電車の速度の問題の考え方・解き方 も読んでみて下さい。

あわせて読みたい

割合・歩合・百分率の文章問題（算数・数学） も読んでみて下さい。