割合・歩合・百分率の文章問題の解き方(算数・数学)
割合(歩合・百分率)の文章問題
本ページはプロモーションが含まれています

算数・数学の割合に関する問題を解くコツについてお伝えいたします。
割合とは歩合・百分率のことです。
割合の問題が苦手!というお子さんがいましたら、一緒に読んでいただければと思っています。
動画による解説は こちら(クリック)↓
問題1 200gの30%は何gですか?
問題2 400円の4割はいくらですか?
問題1、問題2をすぐに計算して解くことができないお子さんへ。

つまり
問題1 200gの30%倍は何gですか?
問題2 400円の4割倍はいくらですか?
と、考えればよいのです。
30%倍?4割倍?何これ?と思われるでしょう。
そこで次に、歩合(割・分・厘)や百分率(%)を小数で表すのです。
歩合や百分率を小数に直す練習は小学校で行なったと思います。
30%は0.3、4割は0.4なので
問題1 200gの0.3倍は何gですか?
問題2 400円の0.4倍はいくらですか?
と、なります。
よって
問題1 200gの0.3倍、すなわち200×0.3=60
答え.60g
問題2 400円の0.4倍、すなわち400×0.4=160
答え.160円
と、答えを求めることができます。
文章問題で、割合(歩合・百分率)は小数に直す
ここで、歩合や百分率を小数で表す場合の覚え方。
10割は1なので、5割はえーっと0.5で・・・、
と、ただ暗記するより、

買い物に行ったら、特売で5割引だった!つまり半額だった!と覚えたら、覚えやすいのではないでしょうか。
半額ということは、半分なので、1の半分は0.5、
だから5割は0.5
ついでに1割は0.1
分は割のひとつ下の単位だから、1分は0.01、2分は0.02、
と覚えたらどうでしょう?

また、百分率は、単位は%ですが、この『%』の真ん中の線を左に移動すると100という形になりますね。

ですから100%が1、よって10%は0.1、1%は0.01、
と覚えたらどうでしょう?
2割引き、とか、30%引き、という計算ができない子が増えているように感じます。
お母さんと一緒に、チラシを見たり、買い物に行ったり、レシートを見れば、関心が出て割合の問題もできるようになるでは、と思っています。
では次にやや難しい問題を考えてみましょう。
【問題】 定価税込800円の商品を30%引きで売っていましたが売れ残ってしまったため、売り値の20%引きで販売しました。この商品は何円で販売しましたか?
この問題は定価の30%引きで売ったが売れ残ったので、さらに20%引きで販売した、という問題です。そして最後に販売した価格を求めます。
図で表すと次のようになります。
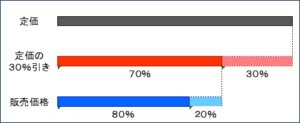
はじめ定価の30%引きで売ったということは、定価の70%で売ったということです。
次に定価の70%の値段をさらに20%引きにしたということは、定価の70%の値段の80%を販売価格にしたということです。
定価が800円なので、はじめに売った値段は
800×0.7=560(円)
次に560円の80%で売ったので販売価格は
560×0.8=448(円) 答え.448円
となります。
しかし1つ1つ計算するより、まとめて計算する方が、簡単にできます。
30%引きは計算の時は(1-0.3)を使い、20%引きは(1-0.2)を使います。
定価800円の商品を30%引きした後にそれを20%引きにするわけですから
800×(1-0.3)×(1-0.2)=448
答え.448円
慣れたらこの式を使ってみて下さい。
食塩水の濃度の解き方、考え方のコツ

最後に、算数や数学でよく出題される食塩水の濃度に関する問題を解くコツ、考え方のコツをお伝えします。
食塩水の濃度を求める式は、$\frac{食塩}{食塩水}$×100(%) です。
これは全体(食塩水)の中に入っている食塩の割合を表しています。
式の意味を理解している子はどんな問題も解くことができますが、式を丸暗記しているだけの子は問題によって解けたり解けなかったりしてしまいます。
例えば、60gの水に4gの食塩を入れると食塩水の濃度は何%になりますか?
よく読めば気がつくのですが、60gの水に4gの食塩を加えたので、全体の量すなわち食塩水は60+4=64(g)です。ですから分母は64。しかし64gではなく60gで計算してしまう、つまり分母を60で計算してしまうのです。
このようなケアレス・ミスをなくすために、食塩水の濃度を求める式を、$\frac{食塩}{食塩+水}$×100(%) と覚えると、わかりやすくなりミスがなくなります。
つまり食塩水という表現を使わず、代わりに(食塩+水)という表現にするのです。
是非こちらの表現をお子さんにおすすめしてみて下さい。
算数が苦手な子が得意になる近道の問題集 ↓
あわせて読みたい
『デイリー算数』 は小学3年生~小学6年生のプリント形式の問題集です。1学年分で約170枚あり、繰り返し練習できるようにPDF形式です。小学生のうちに『デイリー算数』の問題を全て解けるようになれば中学の数学でも高得点を取ることができます。
→ 詳細はこちら
あわせて読みたい
算数・数学の文章問題を解くコツ も読んでみて下さい。
あわせて読みたい
速さに関する文章問題を解くコツ も読んでみて下さい。
勉強方法関連は こちら です。









最近のコメント