通過算、電車が走る速度と時間、速さの問題の考え方・解き方、算数・数学
算数・数学で速さ・時間・道のりを求める問題があります。速度（時速・分速・秒速）の意味を理解して、問題の状況をイメージしたり、図に書ければ楽に解くことができます。
速度とは？
本ページはプロモーションが含まれています
速度は秒速・分速・時速などで表します。
秒速…速さを１秒間に進んだ道のりで表したもの。
（例えば、秒速5ｍとは1秒間に5ｍ進む速さのこと）。
分速…速さを１分間に進んだ道のりで表したもの。
（例えば、分速300ｍとは1分間に300ｍ進む速さのこと）。
時速…速さを１時間に進んだ道のりで表したもの。
（例えば、時速18kmとは1時間に18km進む速さのこと）。
秒速5mとは1秒間に5m進む速さなので、
60秒では5mの60倍 → 5×60＝300m進みます。
60秒＝1分 よって 秒速5m＝分速300m です。
分速300mとは1分間に300m進む速さなので、
60分では300mの60倍 → 300×60＝18000m(18km)進みます。
60分＝1時間 よって 分速300m＝時速18km です。
基本から着実に理解して
格段に成績を伸ばす「すらら」↓
通過算
動画による解説は こちら（クリック）↓
電車がトンネルを通過（１）
【問題】長さ２０ｍの電車が、長さ２２０ｍのトンネルに入り始めてから完全にトンネルを出るまでに８秒かかりました。この電車の速さは秒速何ｍでしょうか。また時速何ｋｍでしょうか。
上図のＡがトンネルに入り始めたところ、Ｂが完全にトンネルを出たところです。
よってＡからＢまで進んだ距離がわかれば問題を解くことができます。
電車のように長さのあるものが進んだ距離を求めるには、どこか１点を決めてそれが進んだ距離を求めればいいのです。
下図では１点を電車の先頭（赤い点）として、その移動距離を求めた図です。
電車はＡからＢへ進むのに８秒かかったわけですから、
（２２０＋２０）÷８＝３０ 答え．秒速３０ｍ
１時間＝３６００秒
電車は１秒で３０ｍ進むので、３６００秒では
３０×３６００＝１０８０００
１０８０００ｍ＝１０８ｋｍ 答え．時速１０８ｋｍ
基本から着実に理解して
格段に成績を伸ばす「すらら」↓
電車がトンネルを通過（２）
【問題】長さ３０ｍの電車が、長さ３８０ｍのトンネルを通過するときにトンネルに完全に隠れている時間が１４秒間でした。この列車の速さは秒速何ｍでしょうか。また時速何ｋｍでしょうか。
上図のＡがトンネルに完全に入ったところ、Ｂがトンネルから出るところです。
よってＡからＢまでが完全に隠れている状態でこの距離がわかれば問題を解くことができます。
電車のように長さのあるものが進んだ距離を求めるには、先ほどと同様にどこか１点を決めてそれが進んだ距離を求めればいいのです。
下図では１点を電車の先頭（赤い点）として、その移動距離を求めた図です。
電車はＡからＢへ進むのに１４秒かかったわけですから、
（３８０ー３０）÷１４＝２５ 答え．秒速２５ｍ
１時間＝３６００秒
電車は１秒で２５ｍ進むので、３６００秒では
２５×３６００＝９００００
９００００ｍ＝９０ｋｍ 答え．時速９０ｋｍ
基本から着実に理解して
格段に成績を伸ばす「すらら」↓
電車が電柱を通過
【問題】長さ２４０ｍの電車が、電柱を通過するのに６秒かかりました。この電車の速さは秒速何ｍでしょうか。また時速何ｋｍでしょうか。（ただし電柱の太さは考えません。）
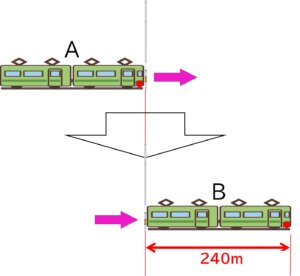
上図のＡが電柱に差しかかるところ、Ｂが電柱を通過し終わったところです。
よってＡからＢまで進んだ距離がわかれば問題を解くことができます。
電車のように長さのあるものが進んだ距離を求めるには、先ほどと同様にどこか１点を決めてそれが進んだ距離を求めればいいのです。
上図では１点を電車の先頭（赤い点）として、その移動距離を求めた図です。
図を見ればわかりますが、移動距離＝電車の長さ になります。
電車はＡからＢへ進むのに６秒かかったわけですから、
２４０÷６＝４０ 答え．秒速４０ｍ
１時間＝３６００秒
電車は１秒で４０ｍ進むので、３６００秒では
４０×３６００＝１４４０００
１４４０００ｍ＝１４４ｋｍ 答え．時速１４４ｋｍ
→ 詳細はこちら
（クリック）↓↓
基本から着実に理解して
格段に成績を伸ばす「すらら」↓
あわせて読みたい
速さに関する文章問題を解くコツ も読んでみて下さい。
あわせて読みたい
算数・数学の文章問題を解くコツ も読んでみて下さい。
あわせて読みたい
割合・歩合・百分率の文章問題（算数・数学） も読んでみて下さい。
勉強方法関連は こちら です。